Обнаружение ошибок
Для обнаружения ошибок в передаваемых данных в общем случае могут применяться различные методы. К ним, в частности, относятся:
- посимвольный контроль четности (используемый при передаче по порту RS-232);
- поблочный контроль четности;
- расчет контрольной суммы;
- контроль циклическим избыточным кодом (CRC).
Реализация первых трех методов относительно проста. К сожалению, неспособность этих методов выявлять группирующие ошибки ограничивает их практическую применимость.
CRC-контроль является более мощным методом обнаружения ошибок и используется для обнаружения ошибок на уровне блоков данных. Он основан на делении и умножении многочленов. В определенном смысле CRC-контроль является алгоритмом хеширования, который отображает (хэширует) элементы большого набора на элементы меньшего набора. IIpoiiecc хэширования приводит к потере информации. Хотя каждый отдельный элемент набора данных отображается на один и только один элемент хэш-набора — обратное не верно. При CRC-контроле большой набор всех возможных двоичных чисел отображается на меньший набор всех возможных CRC.
Вычисление и использование кода CRC производится в соответствии со следующей последовательностью действий:
К содержимому кадра, описываемого полиномом F(x), добавляется набор единиц 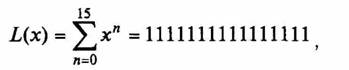
количество которых равно длине поля CRC.
Образованное таким образом число х F(x)+x L(x), где k — степень F(x), делится на производящий полином д(х).
Остаток 0(х) от такого деления, определяемый из соотношения
Q(x)g(x)=x16 F(x)+xkL(x) + 0(х),
где Q(x) — частное от деления x16F(x)+xkL(x) на д(х), в инвертированном виде помещается в контрольное поле кадра.
На приемной стороне выполняется деление содержимого кадра с полем CRC xl6F'(x)+xkL(x) + 0(х), где F'(x)=xi6F(.x)+L(x)+0(x) - передаваемая кодовая комбинация, на полином д(х). Результат такого деления можно привести к виду:
xVF(x)+xkL(x)+0(x)]/g(y>xwL(xVg(x)=xi\Q(x)g(x)}/g(x)+xlбUx)/g(x).
Числитель первого слагаемого делится па д(х), поэтому в приемнике, если при передаче ве было ошибок, остаток получается равным остатку от деления постоянного числителя второго слагаемого (х1 L(x)/g(x)) и имеет вид
x^+x^+x^x^xV+x+i = 1110100001111.
Таким образом, если результат вычислений на приемной стороне равен некоторому определенному числу (в некоторых системах нулю, либо другому числу, несовпадающему с приведенным выше), то считается, что передача выполнена без ошибок.
Возможны и другие алгоритмы формирования и проверки контрольного поля кадра. Однако отличия их от рассмотренного носят частный характер.
При выборе порождающего полинома руководствуются желаемой разрядностью остатка и его способностью выявлять ошибки. Ряд порождающих полиномов принят международными организациями в качестве стандартов.
Рекомендацией ITU-T V.41 стандартизуется полином д(х)= х^+х^+х5-^}. Часто этот полином обозначают просто как ССГГТ-16 или МККТТ-16. Он, в частности, используется в протоколе XModem-CRC и производных от него протоколах передачи файлов.
Другим популярным 16-разрядным порождающим полиномом является полином CRC-16. Он приобрел широкую известность как часть протокола двоичной синхронной передачи (BSC — Binary Synchronous Communications) фирмы IBM, Данный многочлен также определяется альтернативной процедурой Приложения А к стандарту V.42 ITU-T. Полином CRC-16 представляется в виде
g(x)=xlб+xi5+x2+i.
Увеличение числа разрядов CRC-поля позволяет значительно повысить надежность передаваемых данных. Порождающий полином CCITT^32 (MKKTT-32) дает 32-разрядный остаток и также стандартизирован в Рекомендации V.42. Многочлен CCITT-32, известный как CRC-32, представляется в виде
g(x)=xз2+xW+xlб+xl2+xll+xlo+xв+x7+ х^+х^х1^.
Находит применение и многочлен CRC-12 g(x)=xi2+xil+xз+\. Он может использоваться в тех случаях, когда для поля CRC выделяется меньшее число разрядов или когда не требуется более высокая точность более длинных CRC.
Техническая реализация вычислений CRC основана, как правило, на использовании сдвиговых регистров с логическими элементами "исключающее ИЛИ" (сумма по модулю 2). Схема деления входной последовательности на полином g(x)=xl6+xl2+x5•<-'^ приведена на рис. 7.3.
После сдвига всего исходного кадра в ячейках памяти сдвигового регистра остается результат деления (остаток). В дальнейшем он используется в качестве контрольного поля кадра.
Таким образом обеспечивается кодовая прозрачность. Протоколу безразлично, какие кодовые комбинации находятся в потоке данных. Единственное, что требуется, так это поддержание уникальности флагов.
Для обнаружения ошибок в передаваемых данных в общем случае могут применяться различные методы. К ним, в частности, относятся:
- посимвольный контроль четности (используемый при передаче по порту RS-232);
- поблочный контроль четности;
- расчет контрольной суммы;
- контроль циклическим избыточным кодом (CRC).
CRC-контроль является более мощным методом обнаружения ошибок и используется для обнаружения ошибок на уровне блоков данных. Он основан на делении и умножении многочленов. В определенном смысле CRC-контроль является алгоритмом хеширования, который отображает (хэширует) элементы большого набора на элементы меньшего набора. Процесс хэширования приводит к потере информации. Хотя каждый отдельный элемент набора данных отображается на один и только один элемент хэш-набора — обратное не верно. При CRC-контроле большой набор всех возможных двоичных чисел отображается на меньший набор всех возможных CRC.
Вычисление и использование кода CRC производится в соответствии со следующей последовательностью действий:
К содержимому кадра, описываемого полиномом F(x), добавляется набор единиц
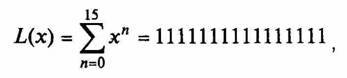
количество которых равно длине поля CRC.
Образованное таким образом число x16F(x)+x L(x), где k — степень F(x), делится на производящий полином д(х).
Остаток 0(х) от такого деления, определяемый из соотношения
Q(x)g(x)=x16 F(x)+xkL(x) + 0(х),
где Q(x) — частное от деления x16F(x)+xkL(x) на д(х), в инвертированном виде помещается в контрольное поле кадра.

Рис. 7.3. Схема деления на полином g(x)=x +x +х +1